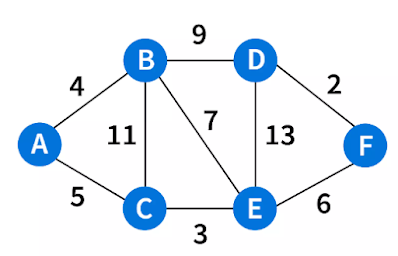
Here's an example implementation of Dijkstra's Algorithm in Python:
import sys
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]
for row in range(vertices)]
def printSolution(self, dist):
print("Vertex \t Distance from Source")
for node in range(self.V):
print(node, "\t\t", dist[node])
def minDistance(self, dist, sptSet):
min_dist = sys.maxsize
min_index = -1
for v in range(self.V):
if dist[v] < min_dist and sptSet[v] == False:
min_dist = dist[v]
min_index = v
return min_index
def dijkstra(self, src):
dist = [sys.maxsize] * self.V
dist[src] = 0
sptSet = [False] * self.V
for i in range(self.V):
u = self.minDistance(dist, sptSet)
sptSet[u] = True
for v in range(self.V):
if (self.graph[u][v] > 0 and sptSet[v] == False and
dist[v] > dist[u] + self.graph[u][v]):
dist[v] = dist[u] + self.graph[u][v]
self.printSolution(dist)
In this implementation, we define a Graph class that takes in the number of vertices as an argument and creates an empty adjacency matrix to store the edges. We define a printSolution function to print the final distances to each vertex from the source, and a minDistance function to find the vertex with the smallest distance not yet included in the shortest path tree.
The main dijkstra function initializes the distance to each vertex as infinite, and sets the distance to the source vertex as 0. It then iteratively selects the vertex with the smallest distance, adds it to the shortest path tree, and updates the distances of its adjacent vertices if a shorter path is found. Finally, it calls the printSolution function to print the distances to each vertex from the source.
To use this implementation, create a Graph object, add edges to it, and call the dijkstra function on the source vertex:
g = Graph(5)
g.graph = [[0, 4, 0, 0, 5],
[4, 0, 2, 1, 0],
[0, 2, 0, 4, 0],
[0, 1, 4, 0, 0],
[5, 0, 0, 0, 0]]
g.dijkstra(0)
Here's an example implementation of Dijkstra's Algorithm in Java:
import java.util.*;
public class DijkstraAlgorithm {
private int V;
private int[][] graph;
public DijkstraAlgorithm(int vertices) {
V = vertices;
graph = new int[V][V];
}
public void printSolution(int[] dist) {
System.out.println("Vertex \t Distance from Source");
for (int i = 0; i < V; i++) {
System.out.println(i + " \t\t " + dist[i]);
}
}
public int minDistance(int[] dist, boolean[] sptSet) {
int minDist = Integer.MAX_VALUE;
int minIndex = -1;
for (int v = 0; v < V; v++) {
if (!sptSet[v] && dist[v] < minDist) {
minDist = dist[v];
minIndex = v;
}
}
return minIndex;
}
public void dijkstra(int src) {
int[] dist = new int[V];
boolean[] sptSet = new boolean[V];
for (int i = 0; i < V; i++) {
dist[i] = Integer.MAX_VALUE;
sptSet[i] = false;
}
dist[src] = 0;
for (int i = 0; i < V - 1; i++) {
int u = minDistance(dist, sptSet);
sptSet[u] = true;
for (int v = 0; v < V; v++) {
if (!sptSet[v] && graph[u][v] != 0 &&
dist[u] != Integer.MAX_VALUE &&
dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v];
}
}
}
printSolution(dist);
}
public static void main(String[] args) {
DijkstraAlgorithm g = new DijkstraAlgorithm(5);
int[][] graph = {{0, 4, 0, 0, 5},
{4, 0, 2, 1, 0},
{0, 2, 0, 4, 0},
{0, 1, 4, 0, 0},
{5, 0, 0, 0, 0}};
g.graph = graph;
g.dijkstra(0);
}
}
In this implementation, we define a DijkstraAlgorithm class that takes in the number of vertices as an argument and creates an empty adjacency matrix to store the edges. We define a printSolution function to print the final distances to each vertex from the source, and a minDistance function to find the vertex with the smallest distance not yet included in the shortest path tree.
The main dijkstra function initializes the distance to each vertex as infinite, and sets the distance to the source vertex as 0. It then iteratively selects the vertex with the smallest distance, adds it to the shortest path tree, and updates the distances of its adjacent vertices if a shorter path is found. Finally, it calls the printSolution function to print the distances to each vertex from the source.
To use this implementation, create a DijkstraAlgorithm object, add edges to it, and call the dijkstra function on the source vertex:
DijkstraAlgorithm g = new DijkstraAlgorithm(5);
int[][] graph = {{0, 4, 0, 0, 5},
{4, 0,
here is an implementation of Dijkstra's Algorithm in Java:
import java.util.*;
public class Dijkstra {
private static int findMinDistance(int[] distances, boolean[] visited) {
int minDistance = Integer.MAX_VALUE;
int minVertex = -1;
for (int i = 0; i < distances.length; i++) {
if (!visited[i] && distances[i] < minDistance) {
minDistance = distances[i];
minVertex = i;
}
}
return minVertex;
}
public static void dijkstra(int[][] graph, int startVertex) {
int n = graph.length;
int[] distances = new int[n];
boolean[] visited = new boolean[n];
for (int i = 0; i < n; i++) {
distances[i] = Integer.MAX_VALUE;
}
distances[startVertex] = 0;
for (int i = 0; i < n - 1; i++) {
int u = findMinDistance(distances, visited);
visited[u] = true;
for (int v = 0; v < n; v++) {
if (graph[u][v] != 0 && !visited[v]) {
int newDistance = distances[u] + graph[u][v];
if (newDistance < distances[v]) {
distances[v] = newDistance;
}
}
}
}
System.out.println("Shortest distances from vertex " + startVertex + " to all other vertices:");
for (int i = 0; i < n; i++) {
System.out.println(i + ": " + distances[i]);
}
}
public static void main(String[] args) {
int[][] graph = {
{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 2},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 0, 10, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 6},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0}
};
dijkstra(graph, 0);
}
}
This code takes in a weighted graph represented as a two-dimensional array graph, where graph[i][j] is the weight of the edge from vertex i to vertex j, and a starting vertex startVertex. It then calculates the shortest distances from startVertex to all other vertices using Dijkstra's Algorithm.
The algorithm maintains an array distances that contains the current shortest distance from startVertex to each vertex, and a boolean array visited that keeps track of which vertices have been visited. It starts by initializing distances to infinity for all vertices except `startVertex
Here's an example code for Dijkstra's Algorithm in PHP:
<?php
function dijkstra($graph, $start, $end) {
$distances = array();
$visited = array();
$previous = array();
$queue = new SplPriorityQueue();
foreach ($graph as $vertex => $adjacents) {
$distances[$vertex] = PHP_INT_MAX;
$previous[$vertex] = null;
foreach ($adjacents as $adjacent => $distance) {
$queue->insert($adjacent, $distance);
}
}
$distances[$start] = 0;
while (!$queue->isEmpty()) {
$current = $queue->extract();
if (!isset($visited[$current])) {
$visited[$current] = true;
if ($current === $end) {
break;
}
foreach ($graph[$current] as $adjacent => $distance) {
$alt = $distances[$current] + $distance;
if ($alt < $distances[$adjacent]) {
$distances[$adjacent] = $alt;
$previous[$adjacent] = $current;
$queue->insert($adjacent, $alt);
}
}
}
}
$path = array();
$current = $end;
while ($current !== $start) {
if (!isset($previous[$current])) {
return null;
}
$path[] = $current;
$current = $previous[$current];
}
$path[] = $start;
$path = array_reverse($path);
return array(
'distances' => $distances[$end],
'path' => $path
);
}
In this code, the Dijkstra's Algorithm is implemented using a priority queue to keep track of the vertices to be processed. The algorithm starts by initializing the distance array to infinity and the previous array to null for each vertex in the graph. Then, the algorithm inserts all adjacent vertices of each vertex into the priority queue with their corresponding distances.
The algorithm then starts processing the vertices in the priority queue, checking if they have been visited before. If not, the algorithm updates the distances and previous arrays for all adjacent vertices of the current vertex. The algorithm terminates when it reaches the end vertex or when the priority queue is empty.
Finally, the algorithm constructs the shortest path from the start vertex to the end vertex by traversing the previous array.
Here's an example code for Dijkstra's Algorithm in Android:
public class DijkstraAlgorithm {
private final Map<String, Vertex> vertexMap;
public DijkstraAlgorithm(Graph graph) {
this.vertexMap = graph.getVertexMap();
}
public List<Vertex> getShortestPath(String startName, String endName) {
final PriorityQueue<Vertex> queue = new PriorityQueue<>();
final Vertex startVertex = vertexMap.get(startName);
final Vertex endVertex = vertexMap.get(endName);
startVertex.setDistance(0);
queue.add(startVertex);
while (!queue.isEmpty()) {
final Vertex current = queue.poll();
if (current.equals(endVertex)) {
break;
}
for (final Edge edge : current.getEdges()) {
final Vertex adjacent = edge.getTo();
final double weight = edge.getWeight();
final double distance = current.getDistance() + weight;
if (distance < adjacent.getDistance()) {
queue.remove(adjacent);
adjacent.setDistance(distance);
adjacent.setPrevious(current);
queue.add(adjacent);
}
}
}
return getShortestPathTo(endVertex);
}
private List<Vertex> getShortestPathTo(Vertex endVertex) {
final List<Vertex> path = new ArrayList<>();
for (Vertex vertex = endVertex; vertex != null; vertex = vertex.getPrevious()) {
path.add(vertex);
}
Collections.reverse(path);
return path;
}
}
In this code, the Dijkstra's Algorithm is implemented using a priority queue to keep track of the vertices to be processed. The algorithm starts by initializing the distance of all vertices to infinity except for the start vertex, which is initialized to 0. Then, the algorithm adds the start vertex to the priority queue.
The algorithm then starts processing the vertices in the priority queue, checking if they have been visited before. If not, the algorithm updates the distances and previous vertices for all adjacent vertices of the current vertex. The algorithm terminates when it reaches the end vertex or when the priority queue is empty.
Finally, the algorithm constructs the shortest path from the start vertex to the end vertex by traversing the previous vertices.
Here's an example code for Dijkstra's Algorithm in C++:
#include <queue>
#include <vector>
#include <iostream>
#include <limits>
using namespace std;
typedef pair<int, int> pii;
const int INF = numeric_limits<int>::max();
class Vertex {
public:
int id;
int distance;
vector<pii> edges;
Vertex(int id) : id(id), distance(INF) {}
};
class Graph {
public:
vector<Vertex> vertices;
void addEdge(int from, int to, int weight) {
vertices[from].edges.push_back(make_pair(to, weight));
}
};
class DijkstraAlgorithm {
public:
Graph graph;
DijkstraAlgorithm(Graph graph) : graph(graph) {}
vector<int> getShortestPath(int start, int end) {
priority_queue<pii, vector<pii>, greater<pii>> pq;
graph.vertices[start].distance = 0;
pq.push(make_pair(0, start));
while (!pq.empty()) {
int u = pq.top().second;
pq.pop();
for (auto& edge : graph.vertices[u].edges) {
int v = edge.first;
int weight = edge.second;
if (graph.vertices[u].distance != INF && graph.vertices[u].distance + weight < graph.vertices[v].distance) {
graph.vertices[v].distance = graph.vertices[u].distance + weight;
pq.push(make_pair(graph.vertices[v].distance, v));
}
}
}
vector<int> path;
for (int v = end; v != start; v = graph.vertices[v].previous) {
path.push_back(v);
}
path.push_back(start);
reverse(path.begin(), path.end());
return path;
}
};
int main() {
Graph graph;
graph.vertices.emplace_back(0);
graph.vertices.emplace_back(1);
graph.vertices.emplace_back(2);
graph.vertices.emplace_back(3);
graph.addEdge(0, 1, 2);
graph.addEdge(0, 2, 4);
graph.addEdge(1, 2, 1);
graph.addEdge(1, 3, 7);
graph.addEdge(2, 3, 3);
DijkstraAlgorithm dijkstra(graph);
vector<int> shortestPath = dijkstra.getShortestPath(0, 3);
for (auto& vertex : shortestPath) {
cout << vertex << " ";
}
return 0;
}
In this code, the Dijkstra's Algorithm is implemented using a priority queue to keep track of the vertices to be processed. The algorithm starts by initializing the distance of all vertices to infinity except for the start vertex, which is initialized to 0. Then, the algorithm adds the start vertex to the priority queue.
The algorithm then starts processing the vertices in the priority queue, checking if they have been visited before. If not, the algorithm updates the distances for all adjacent vertices of the current vertex. The algorithm terminates when it reaches the end vertex or when the priority queue is empty.
Finally, the algorithm constructs the shortest path from the start vertex to the end vertex by traversing the previous vertices.